Proxy-Modeling of Alternative Investments

How often do you find you don’t have quite the right wrench in your toolbox? Axioma Risk, our multi-asset class risk system, provides risk measures on investments in exchange traded assets, factor-level decomposition, and stress tests that can be adjusted to reflect current market concerns. But what if the portfolios you oversee have a small number of investment types for which Axioma Risk does not seem to have quite the right built-in model, such as timberland exposures, marginal holdings in certain hedge-funds for which you do not have position-level transparency, or holdings in private equity funds? In certain cases, time-series of returns on the asset are available. In other cases, you may not have a return time-series, but you do have an intuition of the factors that may drive return. Enter the Axioma Risk factor selection model.

Axioma Risk’s factor selection model was designed to provide users with a stop-gap solution when there is no pre-defined asset return (usually risk neutral pricing) model for an investment. The model allows users to generate risk reports showing exposures to factors that they have chosen, and can be used with factors from Axioma’s Robust Equity Models, fixed-income factors, such as yield curve nodes, commodity factors, or any of the granular market-related factors on the platform (for example, credit spreads, FX-rates, or implied volatilities). The analytics that appear in the reports cover almost all the computations supported by the application and include: risk measures such as VaR or CVaR computed using parametric or simulation-based methods, all forms of stress testing, and sensitivity measures, such as FX01 or DV01.

The model allows users to set up a set of ‘candidate’ factors that they believe may drive returns on their investment. To use the factor selection process, a user must provide a time-series of asset returns or asset price history. The frequency of the asset return time-series may be at the same sampling frequency or a lower frequency than the factor returns. The factor selection engine chooses a subset of the candidate factors, a linear combination of which best reproduce the returns on the asset.

Use Case: Approximating Private Equity Exposure

In recent years, there has been a growing trend to allocate a small portion of balanced portfolios in alternative asset classes, such as private equity. Typically, asset owners may hold 15-25% overall in such alternatives, with perhaps 5% in private equity, executing the investment using private equity funds. Investments are usually long term, with holding periods of 5-7 years. One of the issues associated with this asset class is the lack of a liquid secondary market, and realistic revaluation of the underlying assets may only occur as the fund engages in a financing round or when an investor exits. At times between these events, the general managers of a fund may mark-to-market using a mixture of historical and current prices, which tends to result in somewhat ‘smooth’ return time-series compared with the returns of publicly traded equity vehicle, such as an equity ETF. Hence, naively computing correlations with public equities will lead to poor betas and under-estimates of risk.

Risk models for private equity should reflect the fact that the fund is closed-ended with finite life. Two approaches are typically adopted for risk-modeling such investments:

1. Discounted cash-flow projections are assembled in a top-down manner using past flows from similar funds or in a bottom-up manner based on actual investments, the latter approach being exceedingly difficult due to lack of relevant information for the analysis and the complexity of constructing the flows.
2. For funds where the volatility of the fund is represented primarily by the risks in the underlying portfolio companies rather than entry or exit timings, or where an investor has limited exposure to private equity, using a NAV-based methodology is likely appropriate. Such an approach is simple and is likely to give a good approximation of risk. This is more typically the case for later stage investments.

Modeling in Axioma Risk

As highlighted, Axioma Risk includes a model, based on a form of forward factor selection, which can be used to create a proxy model for a private equity holding using approach (2) listed above. Indeed, a cash-flow based model can be constructed by creating a sequence of cash-flows with the platform’s over-the-counter asset pricing models, but such an approach is out of the scope of this note. The model was provided with a return time-series for a Private Equity fund. We also provided four candidate factor returns, comprised of equity returns that are closely associated with the strategy underlying the fund’s investments.

The factor selection model, called “Linear Model” in the application, relates the price time series of the instrument (response) to a set of significant factors (regressors) using a Stepwise Regression approach.

where y is the response variable, x⁽ⁱ⁾’s are the available risk factors and β⁽ⁱ⁾’s are the regression coefficients.

The model chooses a subset of factors from the candidate factor universe provided by the user. The user also has the option of guiding the factor selection procedure by specifying

• the initial set of factors in the Stepwise Regression,
• a subset of the factors that can be forced to be included in the approach, and
• the conditions under which the factors enter or leave the selection set.

Within Axioma Risk, in the Admin tab, you can create the Linear Model instrument by navigating to Instruments → Instruments Definition → Instrument (see Figure 1).

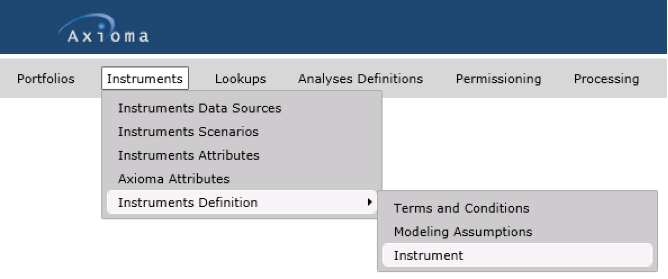
Figure 1 – Finding the Instrument set-up menu in Axioma Risk

You may then select LinearModel in the instrument list under the Editor section in order to set up the proxy instrument (see Figure 2).

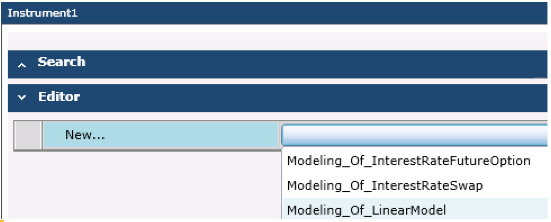
Figure 2 – Selecting the Linear Model Instrument Type

An editor allowing a user to define a Linear Model instrument appears. You can provide a name for the instrument (the DataId field gets populated automatically) and click on the button to the right of the TermsAndConditions field in order to set up the terms and conditions. All fields marked in bold in the UI are mandatory.

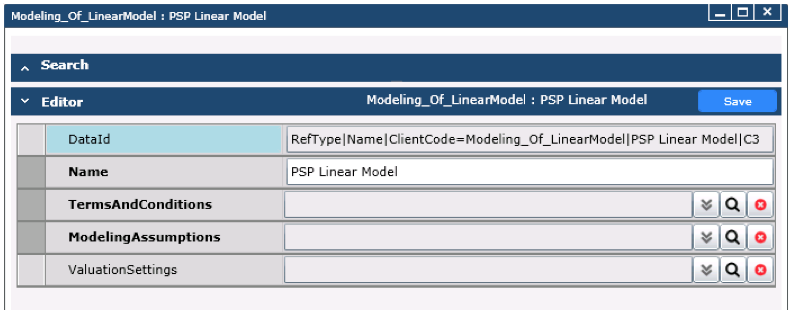
Figure 3 – Initial dialogue screen for creating a Linear Model

The TermsAndConditions editor allows you to specify the inputs for running the stepwise regression, such as the time series of the asset returns (dependent variable) to be modeled and the factor universe (used as the regressors or independent variables).

Click on FactorsUniverse to create your list of candidate factors.

Figure 4 – Adding Candidate Factors

You have the option of searching for and choosing existing factors that Axioma covers (like a price time series of a stock or an interest rate time series) by clicking , or you can load in your own set of price time series for factors by clicking .

You can search for a PriceTimeSeries_Of_Stock for Apple, Inc. by just typing AAPL in the search field. The Apple price series will now be part of the factor universe (see Figure 4). In this way, you can add as many factors as required. The same procedure can be followed if you wish to define a set of InitialFactors and RequiredFactors (factors that you are certain that you wish include in the Linear Model). You can select the sampling frequency of your asset return data, for example daily, weekly, or monthly.

It can be assumed that daily data for several instruments, such as hedge funds and private equity, are not available publicly. It can also be assumed daily data is available for the factors (regressors). Axioma Risk incorporates a method where a mixed frequency correction is applied to the least squares covariance matrix. This allows the user to obtain a better estimate than if only the low frequency data had been used.

Click the  button to the right of the ResponsePriceTimeSeriesId field. This provides a dialogue where you may enter a price series for the asset. You may copy a time series from Microsoft Excel™ and paste it into the Observations field. Of course, the Axioma Risk API provides a convenient mechanism to upload such time-series in an automated manner from back-end systems. The PricingCurrencyId is a mandatory field and you can choose a currency that already exists in the database. Click  and type the 3-letter currency code in the search field. You can choose the appropriate currency that appears from the list.

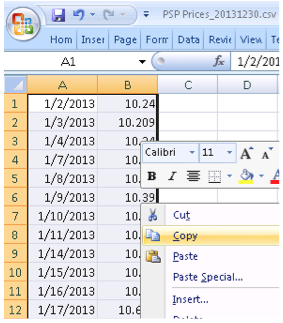
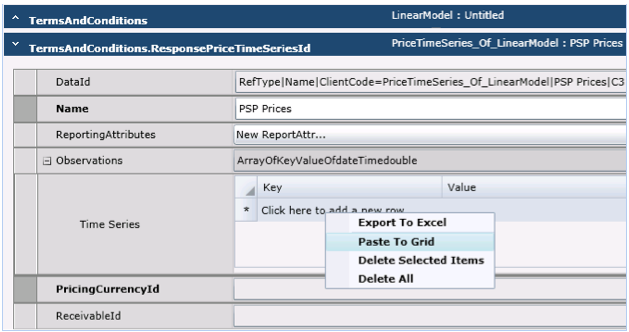
Figure 5 – Pasting in Asset Price History from Excel™

Save the ResponsePriceTimeSeriesId and the TermsAndConditions.

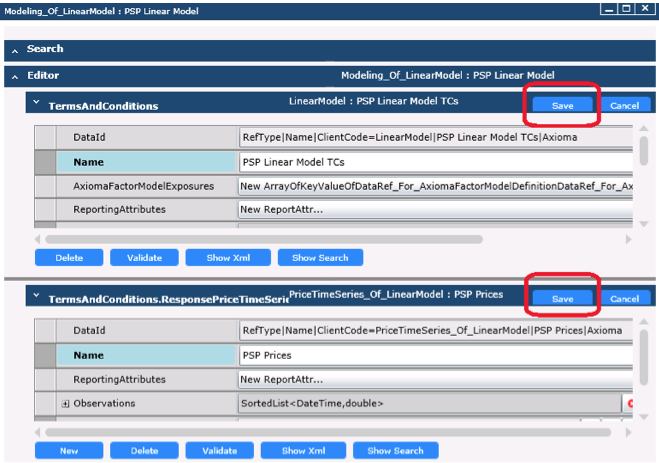
Figure 6 – Saving Configuration

Modeling Assumptions allow the user to define the configuration of factor selection process. Using the Linear Model Editor, click  to the right of the ModelingAssumptions. In the ModelingAssumptions editor, provide a name and create a new CalibrationMethods object. Choose LinearModelCalibrator as the Base. You can uncheck KeepInitialFactors if you do not wish to forcefully include the initial factors in the final model. If you wish to configure in a more detailed manner the conditions for entry into/exclusion of factors from the asset return model, you would need to set up p-values, namely StepWiseRegressionPEnter and StepWiseRegressionPExit. During the regression, the application conducts hypothesis testing on each of the factors to check if the factors are not related to the instrument. The null hypothesis, and alternate hypothesis,  are given below,

where β⁽ⁱ⁾ refers to the regression coefficients for the factors. If the p-value for a factor is less than StepWiseRegressionPEnter, then that factor is included in the linear model. If the p-value for a factor is greater than StepWiseRegressionPExit, then that factor is excluded from the linear model.

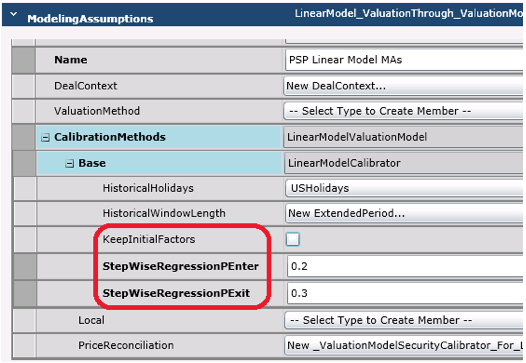
Figure 7 – Modeling Assumptions setup

Save the Modeling Assumptions and the Instrument. Once that is complete, you can create a portfolio containing the Linear Model instrument and run a risk report. Figure 8 shows a Stress Tests report. As can be seen, the Market Value of the instrument, calculated using the regression parameters on 12/31/2013 is $12,038,574 for one million instruments, which is very close to the actual value on that date. Since the underlying factors are equities, we find that the Lehman Collapse of 2008 negatively impacted the Linear Model portfolio as a % of its Total Market Value while shocking the equities by +10% had a positive impact.

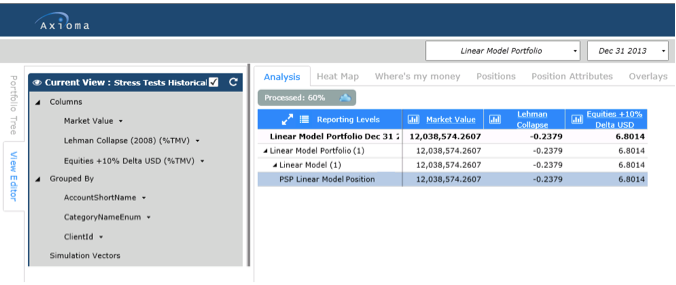
Figure 8 – Report

Conclusion

Axioma Risk offers a way for users to proxy a price time series of instruments that are hard to model due to a lack of data and publicly available information.

By judicious choice of candidate factors, a relevant set of equity exposures may be constructed. Obviously, such an approach does not capture some of the most commonly perceived risks in private equity investing, such as those associated with entry and exit timing, or the dominant fat-tailed, highly idiosyncratic risk profile faced by early stage investors. In the former case, one can plausibly argue that the timing risks are operating on time-scales beyond the horizon of a short-to-medium term market risk model and therefore should be incorporated separately in an enterprise risk oversight process.

The proxy approach is better suited to funds whose primary strategy is medium-large buyouts or mezzanine debt, and is less applicable to seed or early stage funding strategies. Additional sources of risk that may be overlooked by the proxy method we have outlined include:

• Private equity indices or equity returns are typically not very representative of the portfolio held by an investor, or the fund holding companies;
• PE investors who are in fact limited partners in the fund have exposure to the funds undrawn commitments and future use of their distributions.

The Factor Selection Model is a weapon in the risk manager’s arsenal. Our model works consistently with all analytics on the platform.